Estadistica
sábado, 25 de septiembre de 2010
DISTRIBUCION BINOMIAL
Distribuciones discretas
Esperanza matemática o media
Varianza
Desviación típica

0 ≤ pi ≤ 1
p1 + p2 + p3 + · · · + pn = Σ pi = 1
Distribución binomial

n es el número de pruebas.
k es el número de éxitos.
p es la probabilidad de éxito.
q es la probabilidad de fracaso.
El número combinatorio 

Media
Varianza
Desviación típica
Ejercicios
La última novela de un autor ha tenido un gran éxito, hasta el punto de que el 80% de los lectores ya la han leido. Un grupo de 4 amigos son aficionados a la lectura:
1. ¿Cuál es la probabilidad de que en el grupo hayan leido la novela 2 personas?
B(4, 0.8) p = 0.8 q = 0.2

2.¿Y al menos 2?

Un agente de seguros vende pólizas a cinco personas de la misma edad y que disfrutan de buena salud. Según las tablas actuales, la probabilidad de que una persona en estas condiciones viva 30 años o más es 2/3. Hállese la probabilidad de que, transcurridos 30 años, vivan:
1. Las cinco personas.
B(5, 2/3) p = 2/3 q = 1/3

2.Al menos tres personas.

3.Exactamente dos personas.

Si de seis a siete de la tarde se admite que un número de teléfono de cada cinco está comunicando, ¿cuál es la probabilidad de que, cuando se marquen 10 números de teléfono elegidos al azar, sólo comuniquen dos?
B(10, 1/5)p = 1/5q = 4/5

La probabilidad de que un hombre acierte en el blanco es 1/4. Si dispara 10 veces ¿cuál es la probabilidad de que acierte exactamente en tres ocasiones? ¿Cuál es la probabilidad de que acierte por lo menos en una ocasión?
B(10, 1/4) p = 1/4q = 3/4


En unas pruebas de alcoholemia se ha observado que el 5% de los conductores controlados dan positivo en la prueba y que el 10% de los conductores controlados no llevan aprovechado el cinturón de seguridad. También se ha observado que las dos infracciones son independientes.
Un guardia de tráfico para cinco conductores al azar. Si tenemos en cuenta que el número de conductores es suficientemente importante como para estimar que la proporción de infractores no varía al hacer la selección.
1. Determinar la probabilidad a de que exactamente tres conductores hayan cometido alguna de las dos infracciones.

2. Determine la probabilidad de que al menos uno de los conductores controlados haya cometido alguna de las dos infracciones.

La probabilidad de que un artículo producido por una fabrica sea defectuoso es 0.02. Se envió un cargamento de 10.000 artículos a unos almacenes. Hallar el número esperado de artículos defectuosos, la varianza y la desviación típica.
En una urna hay 30 bolas, 10 rojas y el resto blancas. Se elige una bola al azar y se anota si es roja; el proceso se repite, devolviendo la bola, 10 veces. Calcular la media y la desviación típica.
B(10, 1/3) p = 1/3q = 2/3
Un laboratorio afirma que una droga causa de efectos secundarios en una proporción de 3 de cada 100 pacientes. Para contrastar esta afirmación, otro laboratorio elige al azar a 5 pacientes a los que aplica la droga. ¿Cuál es la probabilidad de los siguientes sucesos?
1. Ningún paciente tenga efectos secundarios.
B(100, 0.03) p = 0.03 q = 0.97

2.Al menos dos tengan efectos secundarios.


3.¿Cuál es el número medio de pacientes que espera laboratorio que sufran efectos secundarios si elige 100 pacientes al azar?

DISTRIBUCION BINOMIAL
Función de probabilidad | |
Función de distribución de probabilidad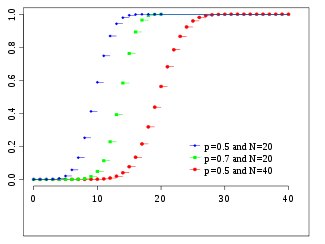 | |
| Parámetros | 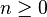 número de ensayos (entero) número de ensayos (entero)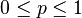 probabilidad de éxito (real) probabilidad de éxito (real) |
|---|---|
| Dominio | 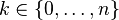 |
| Función de probabilidad (fp) | 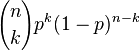 |
| Función de distribución (cdf) | 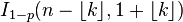 |
| Media | 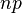 |
| Mediana | Uno de 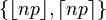 [1] [1] |
| Moda | 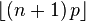 |
| Varianza |  |
| Coeficiente de simetría | 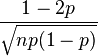 |
| Curtosis |  |
| Entropía | 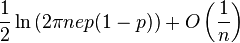 |
| Función generadora de momentos (mgf) |  |
| Función característica | 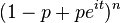 |
Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:
Ejemplos
Las siguientes situaciones son ejemplos de experimentos que pueden modelizarse por esta distribución:- Se lanza un dado 10 veces y se cuenta el número 3 obtenidos: X ~ B(10, 1/6)
- Se lanza una moneda 2 veces y se cuenta el numero de caras obtenidas.
- Una partícula se mueve unidimensionalmente con probabilidad q de moverse hacia atrás y 1-q de moverse hacia adelante
Experimento Binomial
Existen muchas situaciones en las que se presenta una experiencia binomial. Este tipo de experiencias se caracteriza por estar formada por un número predeterminado n de experimentos iguales. Cada uno de los experimentos es independiente de los restantes (la probabilidad del resultado de un experimento no depende del resultado del resto). El resultado de cada experimento ha de admitir sólo dos categorías (a las que se denomina éxito y fracaso). Las probabilidades de ambas posibilidades han de ser constantes en todos los experimentos (se denotan como p y q o p y 1-p).Se designa por X a la variable que mide el número de éxitos que se han producido en los n experimentos.
Cuando se dan estas circunstancias, se dice que la variable X sigue una distribución de probabilidad binomial, y se nota B(n,p).
Características analíticas
Su función de probabilidad es
siendo
 las combinaciones de
las combinaciones de  en
en  (
( elementos tomados de
elementos tomados de  en
en  )
)Propiedades características
Relaciones con otras variables aleatorias
Si n tiende a infinito y p es tal que producto entre ambos parámetros tiende a , entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro λ.
, entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro λ.Por último, se cumple que cuando n es muy grande (usualmente se exige que
 ) la distribución binomial puede aproximarse mediante la distribución normal.
) la distribución binomial puede aproximarse mediante la distribución normal.Propiedades reproductivas
Dadas n variables binomiales independientes, de parámetros ni (i = 1, ..., n) y p, su suma es también una variable binomial, de parámetros n1+ ... + nn, y p, es decir,
Suscribirse a:
Entradas (Atom)

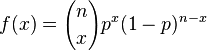
![\mathbb{E}[X] = np\,](http://upload.wikimedia.org/math/9/d/e/9de9fa1e0fe27516979f819fcd341770.png)
![\text{Var}[X] =np(1-p)\,](http://upload.wikimedia.org/math/f/f/9/ff9e94d391080bdb08785b7c4ffd78b0.png)
